Реферат: Астрофизика
зависит от условий обработки. В результате точность фотометрических
измерений, производимых фотографическим методом, обычно не превышает 5-7 %.
Рассмотрим основные типы спектральных приборов, применяемых в астрономии.
Впервые спектры звезд и планет начал наблюдать в прошлом веке итальянский
астроном Секки. После его работ спектральным анализом занялись многие
астрономы. Вначале использовались визуальный спектроскоп, потом спектры стали
фотографировать, а сейчас применяются также и фотоэлектрическая запись
спектра. Спектральные приборы с фотографической регистрацией спектра обычно
называют спектрографами, а с фотоэлектрической – спектрометрами.
На рисунке дана оптическая схема призменного спектрографа. Перед призмой
находятся щель и объектив, которые образуют коллиматор. Коллиматор посылает
на призму параллельный пучок лучей. Коэффициент преломления материала призмы
зависит от длины волны. Поэтому после призмы параллельные пучки,
соответствующие различным длинам волн, расходятся под различными углами, и
второй объектив (камера) дает в фокальной плоскости спектр, который
фотографируется. Если в фокальной плоскости камеры поставить вторую щель, то
спектрограф превратиться в монохроматор. Перемещая вторую щель по спектру или
поворачивая призму, можно выделять отдельные более или менее узкие участки
спектра. Если теперь за выходной щелью монохроматора поместить
фотоэлектрический приемник, то получится спектрометр.
В настоящее время наряду с призменными спектрографами и спектрометрами широко
применяются и дифракционные. В этих приборах вместо призмы диспергирующим
(т.е. разлагающим на спектр) элементом является дифракционная решетка.
Наиболее часто используется отражательные решетки.
Отражательная решетка представляет собой алюминированое зеркало, на котором
нанесены параллельные штрихи. Расстояние между штрихами и их глубина сравнимы
с длинной волны. Например, дифракционные решетки, работающие в видимой
области спектра, часто делаются с расстоянием между штрихами 1,66 мк (600
штрихов на 1 мм). Штрихи должны быть прямыми и параллельными друг другу по
всей поверхности решетки, и расстояние между ними должно сохраняться
постоянным с очень высокой точностью. Изготовление дифракционных решеток,
поэтому является наиболее трудным из оптических производств.
Получая спектр с помощью призмы, мы пользуемся явлением преломления света на
границе двух сред. Действий дифракционной решетки основано на явлении другого
типа – дифракция и интерференция света. Заметим, что она дает, в отличии от
призмы, не один, а несколько спектров. Это приводит к определенным потерям
света по сравнению с призмой. В результате применения дифракционных решеток в
астрономии долгое время ограничивалось исследованиями Солнца. Указанный
недостаток был устранен американским оптиком Вудом. Он предложил придавать
штрихам решетки определенный профиль, такой, что большая часть энергии
концентрируется в одном спектре, в то время как остальные оказываются сильно
ослабленными. Такие решетки называются направленными или эшелеттами.
Основной характеристикой спектрального прибора является спектральная
разрешающая сила
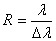 (12) (12)
где Dl - минимальный промежуток между двумя близкими линиями, при котором они
регистрируются как раздельные. Чем больше разрешающая сила, тем более
детально может быть исследован спектр и тем больше информации о свойствах
излучающего объекта может быть в результате получено. Спектральные аппараты с
направленными дифракционными решетками, при прочих равных условиях, могут
обеспечить более высокую разрешающую силу, чем призменные.
Другой важной характеристикой спектральных аппаратов является угловая дисперсия
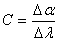 (13) (13)
Где Da - угол между параллельными пучками, прошедшими диспергирующий элемент
и различающимися по длине волны на Dl.
Величина
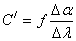 (14) (14)
Где f – фокусное расстояние камеры, называется линейной дисперсией, которая
выражает масштаб спектра в фокальной плоскости камеры и обозначается либо в
миллиметрах на ангстрем, либо (для малых дисперсией) в ангстремах на
миллиметр. Так, дисперсия спектрографа 250 Å/мм, означает, что один
миллиметр на спектрограмме соответствует интервалу длин волн Dl=250Å.
Особенности оптической схемы и конструкции астрономических спектральных приборов
сильно зависит от конкретного характера задач, для которых они предназначены.
Спектрографы, построенные для получения звездных спектров (звездные
спектрографы), заметно отличаются от небулярных, с которыми исследуются спектры
туманностей. Солнечные спектрографы тоже имеют свои особенности. Реальная
разрешающая сила астрономических приборов зависит от свойств объекта. Если
объект слабый, т.е. от него приходит слишком мало света, то его спектр нельзя
исследовать очень детально, так как с увеличением разрешающей силы количество
энергии, приходящей на каждый разрешаемый элемент спектра, уменьшается. Поэтому
самую высокую разрешающую силу имеют, естественно, солнечные спектральные
приборы. У больших солнечных спектрографов она достигает 106.
линейная дисперсия этих приборов достигает 10 мм/Å (0,1 Å/мм).
При исследовании наиболее слабых объектов приходится ограничиваться
разрешающей силой порядка 100 или даже 10 и дисперсиями ~1000 Å/мм.
Например, спектры слабых звезд получаются с помощью объективной призмы,
которая является простейшим астрономическим спектральным прибором.
Объективная призма ставиться прямо перед объективом телескопа, и в
результате изображение звезд растягиваются в спектр. Камерой служит сам
телескоп, а коллиматор не нужен, поскольку свет от звезды приходит в виде
параллельного пучка. Такая конструкция делает минимальными потери света из-за
поглощения в приборе. На рисунке приведена фотография звездного поля,
полученная с объективной призмой.
Грубое представление о спектральном составе излучения можно получить с
помощью светофильтров. В фотографической и визуальной областях спектра часто
применяют светофильтры из окрашенного стекла. На рисунке приведены кривые,
показывающие зависимость пропускания от длины волны для некоторых
светофильтров, комбинируя которые с тем или иным приемником, можно выделить
участки не уже нескольких сотен ангстрем. В светофильтрах из окрашенного
стекла используется зависимость поглощения (абсорбции) света от длины волны.
Светофильтры этого типа называются абсорбционными. Известны светофильтры, в
которых выделение узкого участка спектра основано на интерференции света. Они
называются интерференционными и могут быть сделаны довольно узкополосными,
позволяющими выделять участки спектра шириной в несколько десятков ангстрем.
Еще более узкие участки спектра (шириной около 1 ангстрема) позволяют
выделять интерференционнополяризационные светофильтры.
С помощью узкополосных светофильтров можно получить изображение объекта в
каком-либо интересном участке спектра, например, сфотографировать солнечную
хромосферу в лучах Ha (красная линия в бальмеровской серии спектра водорода),
солнечную корону в зеленой и красной линиях, газовые туманности в эмиссионных
линиях.
Для солнечных исследований разработаны приборы, которые позволяют получить
монохроматические изображения в любой длине волны. Это – спектрогелиограф и
спектрогелиоскоп. Спектрогелиограф представляет собой монохроматор, за
выходной щелью которого находится фотографическая кассета. Кассета движется с
постоянной скоростью в направлении, перпендикулярном выходной щели, и с такой
же скоростью в плоскости выходной щели перемещается изображение Солнца. Легко
понять, что в этом случае на фотографической пластинке получиться изображение
Солнца в заданной длине волны, называемое спектрограммой. В
спектрогелиоскопе, перед выходной щелью и после выходной щели устанавливаются
вращающиеся призмы с квадратным сечением. В результате вращения первой призмы
некоторый участок солнечного изображения периодически перемещается в
плоскости входной щели. Вращение обеих призм согласованно, и если оно
происходит достаточно быстро, то, наблюдая в зрительную трубу вторую щель, мы
видим монохроматическое изображение Солнца.
Развитие физики твердого тела и достижения в области твердотельной технологии
обеспечили возможность промышленного изготовления стабильных фотоприемников,
пригодных для эксплуатации в инфракрасной бортовой оптико-электронной
аппаратуре. Успехи в этих областях знаний позволили создать в последние годы
линейки и матрицы приемников с высокой плотностью чувствительных элементов.
Для формирования выходного сигнала аппаратуры необходимо поочередно измерить
электрические сигналы, поступающие с каждого элемента линейки. Можно сказать,
должно быть обеспечено последовательное подключение электрических проводников
от отдельных элементов к общему выходу.
Путем такого «опроса» чувствительных площадок, расположенных в ряд,
вырабатывается электрический сигнал, соответствующий одной строке
изображения. Процесс переключения электрических цепей чувствительных
элементов в аппаратуре осуществляется специальным электронным переключателем
последовательного действия. В итоге линейка приемников обеспечивает строчное
сканированное изображение электронным, а не механическим способом.
В новейших, наиболее перспективных образцах инфракрасной аппаратуры все чаще
используются твердотельные схемы, обеспечивающие прием и обработку сигнала с
линейки или матрицы в одном устройстве. Первых два коротких сообщения группы
американских исследователей об этой новой идее в области физики твердого тела
и об ее экспериментальной проверке появились в 1970 году. Приборы с зарядовой
связью – так был назван этот класс устройств – привлекали к себе чрезвычайный
интерес и за прошедшие после их изобретения годы нашли самое широкое
применение в устройствах формирования изображений в вычислительной технике, в
устройствах отображения информации.
С точки зрения физики приборы с зарядовой связью интересны тем, что
электрический сигнал в них представлен не током или напряжением, а
электрическим зарядом. Основной принцип их действия изображен на рисунке .
прибор с зарядовой связью представляет собой линейку электродов на изолирующей
основе, нанесенной на поверхность тонкой пластины полупроводника. Обычно под
металлическими под металлическими электродами расположен изолирующий слой
окисла SiO2, а в качестве полупроводникового материала используется
Si. В результате образуется как бы сэндвич: металл – окисел – полупроводник
(рисунок ).
В приборах с зарядовой связью появляется возможность, подавая напряжение на
металлические электроды, воздействовать через изолятор на положение
энергетического уровня, сдвигая его вниз от горизонтальной линии в местах
расположения электродов. В итоге на границе раздела Si – SiO2
энергетическая диаграмма будет представлять собой не ровную, а холмистую
поверхность, на которой впадины будут расположены под теми электродами, к
которым приложено напряжение.
Для наглядности впадины этого рельефа на энергетической диаграмме
представляют в виде ямы с плоским дном и вертикальными стенками. На рисунке
, б изображены такие прямоугольные потенциальные ямы, сформированные с
помощью напряжений, приложенных к электродам. Чем выше напряжение на
электроде, тем глубже яма под данным электродом в месте его расположения.
Когда фотон попадает на чувствительный к излучению Si и создает электронно-
дырочную пару, то электрон стекает в ближайшую потенциальную яму. При
дальнейшем облучении образца электроны будут накапливаться и сохраняться в
соответствующих потенциальных ямах.
Для совокупности электронов, захваченных потенциальной ямой, физики также
придумали образное название, ставшее общепризнанным, - «зарядовый пакет».
Такие зарядовые пакеты в соответствии с изложенным механизмом будут возникать
на поверхности полупроводника
Определение расстояний до тел солнечной системы основано на измерении их
горизонтальных параллаксов. Параллаксы, определенные по параллактическому
смещению светила, называются тригонометрическими.
Зная горизонтальный экваториальный параллакс Pо светила, легко определить его
расстояние от центра Земли (рисунок ). Действительно, если То=Ro есть
экваториальный радиус Земли, ТМ=D - расстояние от центра Земли до светила М,
a угол Р – горизонтальный экваториальный параллакс светила Ро, то из
прямоугольного треугольника ТОМ имеем
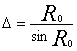 (15) (15)
Для всех светил, кроме луны, параллаксы очень малы. Поэтому формулу (15)
можно написать иначе, положив
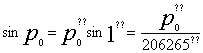 (16) (16)
а именно,
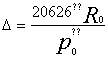 (17) (17)
Расстояние D получается в тех же единицах, в которых выражен радиус Земли Rо. По
формуле (17) определяются расстояния до тел Солнечной системы. Быстрое развитие
радиотехники дало астрономам возможность определять расстояние до тел Солнечной
системы радиолокационными методами. В 1946 году была произведена радиолокация
Луны, а в 1957 – 1963 годах – радиолокация Солнца, Меркурия, Венеры, Марса и
юпитера. По скорости распространения радиоволн с=3*105 км/сек и по
промежутку времени t (сек) прохождения радиосигнала с земли до небесного тела и
обратно легко вычислить расстояние до небесного тела
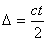 (18) (18)
Расстояние до звезд определяются по их годичному параллактическому смешению,
которое обусловлено перемещением наблюдателя (вместе с Землей) по земной
орбите (рисунок ).
Угол, под которым со звезды был бы виден средний радиус земной орбиты при
условии, что направление на звезду перпендикулярно к радиусу, называется
годичным параллаксом звезды p. Если СТ=a есть средний радиус земной орбиты,
МС=D - расстояние звезды М от солнца С, а угол p - годичный параллакс звезды,
то из прямоугольного треугольника СТМ
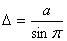 (19) (19)
годичные параллаксы звезд меньше 1¢¢, и поэтому
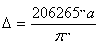 (20) (20)
Расстояние D по этим формулам получается в тех же единицах, в которых
выражено среднее расстояние а Земли от Солнца.
Если расстояние до небесных тел очень велики, то выражать их в километрах
неудобно, так как получается очень большие числа, состоящие из многих цифр,
поэтому в астрономии, помимо километров, приняты следующие единицы
расстояний:
- астрономическая единица (а.е) – среднее расстояние Земли от Солнца;
- парсек (пс) – расстояние, соответствующее годичному параллаксу в 1¢¢;
- световой год – расстояние, которое свет проходит за один год,
распространяясь со скоростью около 300000 км/сек. Если астрономическую единицу
принять равной 149600000 км, то 1 пс=30,86*1012 км= 206263 а.е.=3,26
светового года; 1 световой год=9,460*1012 км=63240 а.е.=0,3067 пс.
В а.е. обычно выражаются расстояния до тел солнечной системы. Например,
Меркурий находится от Солнца на расстоянии 0,387 а.е, а Плутон – на
расстоянии 39,75 а.е.
Расстояние до небесных тел, находящихся за пределами солнечной системы,
обычно выражаются в парсеках, кило парсеках (1000 пс) и мега парсеках
(1000000 пс), а также в световых годах. В этих случаях
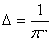 и и 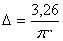
Ближайшая к Солнцу звезда «проксима Центавра» имеет годичный параллакс
p=0¢¢,762. следовательно, она находится от нас на расстоянии 1,31 пс
или 4,26 светового года.
Чтобы перейти от видимого положения звезд на небе к действительному их
распределению в пространстве, необходимо знать расстояние до них.
Непосредственным методом определения расстояния до звезд является измерение их
годичных параллаксов. Однако этим способом параллаксы могут быть найдены только
для ближайших звезд. Действительно, предельные углы, которые удается измерить
аксонометрическими методами, составляют около 0¢¢,01.
Следовательно, если параллакс звезды в результате наблюдений оказался равным
p=0¢¢,02±0¢¢,01, то расстояние до нее по формуле
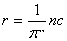 (21) (21)
Получится в пределах от 30 до 100 пс, соответствующих возможным ошибкам в
определении параллакса. Отсюда видно, что расстояние до сравнительно близких
объектов, удаленных от нас не более, чем на несколько парсеков, определяются
более или менее надежно. Так, например, расстояние до одной из ближайших
звезд (a Центавра), равное 1,33 пс, известно с ошибкой, меньше 2 %. Однако
для звезд, удаленных больше чем на 100 пс, ошибка в определении расстояния
больше самого расстояния и метод тригонометрических параллаксов оказывается
непригодным. В лучшем случае он позволяет сделать вывод, что расстояние
превышает несколько сотен парсеков. Всего в настоящее время
тригонометрические параллаксы измерены не более чем для 6000 звезд.
Расстояния до звезд могут быть найдены в тех случаях, когда каким-нибудь
образом известны их светимости, так как разность между видимой и абсолютной
звездными величинами равна модулю расстояния, который входит в формулу (22)
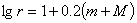 (22) (22)
Наиболее надежно модуль расстояния удается найти для звезд, принадлежащих
скоплениям. Однако при этом необходимо учитывать, что получаемые величины,
как правило, бывают искажены влиянием межзвездного поглощения света.
Особенности спектров, лежащих в основе разделения звезд по классам
светимости, могут быть использованы для определения абсолютных звездных
величин, а, следовательно, и расстояний (метод спектральных параллаксов).
Важный метод определения параллаксов совокупности звезд основан на изучении
их собственных движений. Оставшееся смещение звезды на небесной сфере за год
называется собственным движением звезды m. Оно выражается в секансах дуги в
год. Собственное же движение звезды m вычисляется по формуле
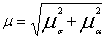 (23) (23)
Собственное движение у разных звезд различны по величине и направлению. Только
несколько десятков звезд имеют собственные движения больше 1¢¢ в год.
Самое большое известное собственное движение m=10¢¢,27 (у «летящей»
звезды Баркарда). Громадное же большинство измеренных собственных движений у
звезд составляют сотые и тысячные доли секунды дуги в год. Из-за малости
собственных движение изменение видимых положений звезд не заметно для
невооруженного глаза.
Суть этого метода основано на том факте, что чем дальше находятся звезды, тем
меньше видимые перемещения, вызываемые их действительными движениями в
пространстве. Определенные таким путем параллаксы называются средними.
Для определения расстояния до группы звезд удается применить наиболее точный
метод, основанный на том обстоятельстве, что, как и в случае метеоритов,
общая точка пересечения направлений видимых индивидуальных движений, которые
вследствие перспективы кажутся различными, а на самом деле в пространстве
одинаковы, указывает истинное направление скорости общего движения – апекс.
При известной лучевой скорости Vr, хотя бы одной из звезд имеется возможность
вычислить годичный параллакс всего скопления, называемый адовым параллаксом,
по формуле
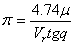 (24) (24)
Где m - собственное движение, а q – угол между направлением на данную звезду
и апекс.
Определить суточный и годичный параллакс можно из наблюдений: пусть из двух
точек О1 и О2 (рисунок ) на поверхности Земли, лежащих
на одном географическом меридиане, измерены зенитные расстояния Z1 и
Z2 одного и того же светила М в момент прохождения его через
небесный меридиан. Предположим далее, что оба пункта наблюдения находятся в
северном полушарии и светило наблюдалось в каждом из них к югу от зенита.
Следовательно
z1=j1-s1 и z2=j2-s2
Где j1 и j2 – географические широты пунктов, а d1
и d2 – топоцентрические скопления светила, отличающиеся от его
геоцентрического склонения d на величину
p1=psinz1 и p2=psinz2
В четырехугольнике О1ТО2М (рисунок ) угол О1МО
2 равен (Р1 – Р2), угол МО2Т тупой
(больше 180º) и равен (180º+Z2), угол О1ТО
2 равен (j1-j2) и, наконец, угол ТО1М
равен (180º-Z1). Так как сумма внутренних углов
четырехугольника равна четырем прямым, то
360°=p1-p2+180°+z2+j1-j2+180°-z
или
p1-p2=(j2-z2)-( j1-z1)
Принимая во внимание соотношения, написанные выше, имеем
P(sinz1-sinz2)={sin(j1-s1)-sin(j2-s2)}p=s2-s1
откуда горизонтальный параллакс светила
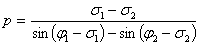 (25) (25)
По значениям радиуса Земли R в месте наблюдения и экваториального радиуса
Земли Rо вычисляется горизонтальный экваториальный параллакс
Страницы: 1, 2, 3, 4, 5
|

